Recently, electric and hybrid vehicles have become increasingly popular because of their internal electric motors, which can provide propulsion and regenerative braking in a unified mechanism. The power-decentralized EV employs independent drive motors to propel the vehicle system. This freedom makes wheel-slip control a crucial issue. Wheel-slip control is a key foundation of the vehicle active safety control system, especially for ESC, which, compared with the ABS and TCS, needs wheel-slip control to generate longitudinal tire force, as well as lateral tire force.
The intrinsic explanation of wheel slip is that the output torque of the actuator exceeds the maximum friction force between the tire and the road surface. However, the friction force cannot be measured directly, and there are changes with regards to the road surface and vehicle states.
To solve this problem in terms of vehicle dynamic control, the implementations available for wheel-slip control fall into two classes: indirect torque control methods based on wheel-slip ratio and direct torque control methods based on the vehicle or wheel model. According to the μ − λ curve, the former methods maintain the optimal wheel-slip ratio in a stable adhesion region to obtain the maximum friction force. To calculate the wheel-slip ratio, the wheel speed is easily detected by a sensor installed on the rotational wheel axle, and the speed of non-driven wheels replace chassis speed for physical and economic reasons.
Clearly, this replacement is not applicable in vehicles without non-driven wheels such as AWD or 4WD systems. No matter how ingenious the chassis speed acquisition is, the result of this indirect method is inherently inaccurate. Although some dedicated sensors can measure the chassis speed directly, they are too sensitive to the environment and too expensive for commercial applications. Therefore, some researchers focus on designing the estimators without the chassis speed. However, these methods are difficult for practical use, and their control robustness is challenged by significant variations in tire-road conditions because they only consider typical road conditions.
On the other hand, distinguished from indirect methods based on wheel-slip ratio, direct methods based on the model of vehicle or wheel do not need information on the chassis speed.
The model following control (MFC) method only makes use of the wheel speed and the motor torque to determine the maximum feedback gain for anti-slip control. Fewer control inputs with a simple control structure facilitate the practicability, low cost, and higher reliability of this method.
However, considering the worst stability situation, such a method impairs the control performance to determine the compensation gain. In addition, the tuned algorithms and parameters are specific to established vehicles or wheel models such that the MFC cannot adapt to the variation in vehicle mass or equivalent vehicle mass transfer. Vehicle wheel slip caused by tire traction deterioration can be compensated by many approaches, such as sliding model control, robust control, fuzzy control, and adaptive control.
The maximum transmissible torque estimation (MTTE) method requires neither the chassis speed nor the tire-road information and takes advantage of a relaxation factor (i.e. the ratio of the vehicle acceleration to the wheel acceleration) to estimate the maximum transmissible torque as the limitation of the motor torque. The MTTE, irrespective of the vehicle mass and road conditions, can restrain the wheel slip effectively. However, the excessively precise torque output limits the practical use of this method.
Consequently, rather than the methods above, a novel wheel-slip control method is proposed that eliminates the acceleration deviation between the actual wheel and the reference wheel center to suppress the wheel-slip trend at the initial stage.
Suggested approach
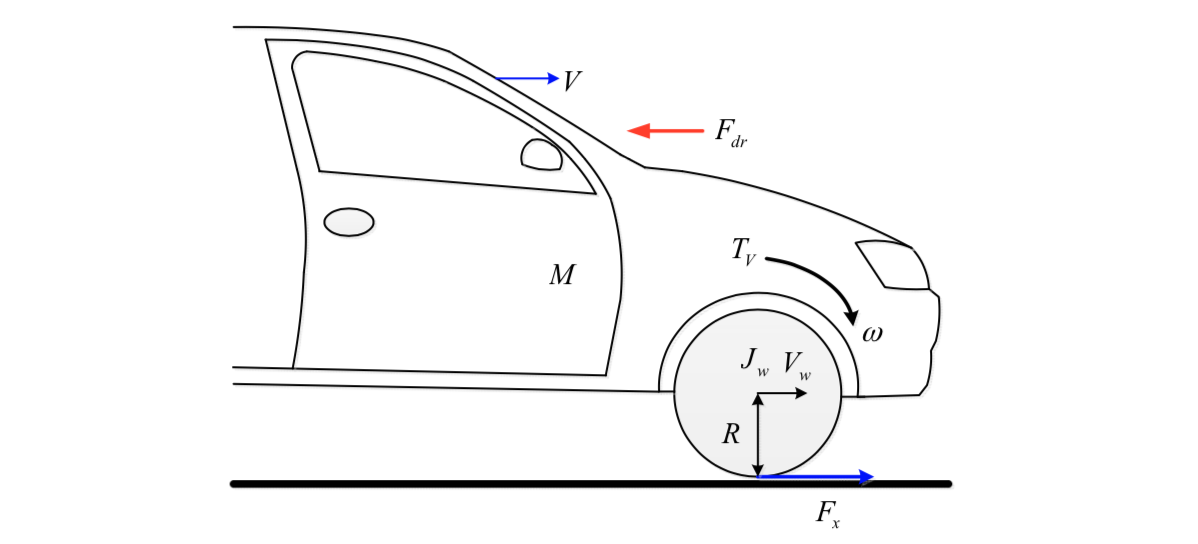
Note that the proposed approach is designed for power-decentralized EVs. Additionally, the vehicle system is assumed to adhere to rigid body dynamics. The dynamics analysis of vehicle longitudinal motion is based on the one-wheel vehicle model, described in Figure 1, while Table 1 lists the parameter definitions.
The dynamics equations for the calculation of the longitudinal vehicle motions are as follows:
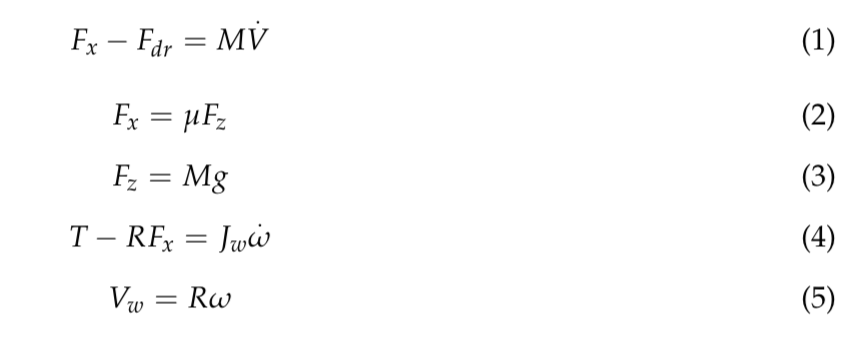
Note that the propulsion torque and braking torque are amalgamated as ‘driving torque T’.

Substituting Equation (5) into Equation (4), the friction force, Fx, can be expressed as:

Assuming that the driving torque T is constant, then, it can be found that the higher the wheel circumferential acceleration Vω, the lower the friction force Fx that can be obtained.
Generally, the friction force is less than the maximum value that the road surface can provide and increases as the drive torque goes up. Based on the tire–friction relations, before the maximum traction force is achieved, the friction force is proportional to the slip ratio. After that, when the slip ratio continues to increase given lateral or longitudinal force, both will deteriorate quickly due to the saturation of the traction force.
Substituting Fx in Equation (1) into Equation (4), the driving torque, including two movements, i.e. the body longitudinal motion and wheel rotation, can be expressed as:

Here, the driving resistance Fdr, which is related to the chassis speed and vehicle shape, is assumed to be zero. Hence:

In conditions where the vehicle runs at high speeds and thus requires higher anti-slip performance, Fdr should be estimated in real time. The regular operation of steering a vehicle can typically be treated as a linear motion, excluding the situation of the vehicle always performing turning control. Consequently, it is easy to see if no slip is expected, i.e. λ = 0; the vehicle acceleration in linear motion then can be obtained as V=ωr=Vω. Therefore, in a pure rolling condition where no slip occurs, the wheel acceleration Vω equals that of the chassis V in Equation (8). When slip starts to occur, i.e., part of the output torque cannot be transmitted to the chassis by the tire-road interaction, the driving torque T containing two parts, can be rewritten as:
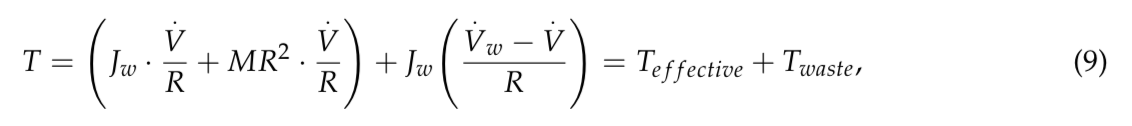
where

Here, Teffective represents the desired maximum torque to maintain a pure rolling state. Twaste stands for extra torque that exists when the slip ratio is not equal to zero. It is invalid torque that does not contribute to the propulsion. It turns into rotational kinetic energy when the wheel self-spins in skidding scenarios. Note that less of the wasted energy may be stored in different areas, such as potential energy in the suspension. However, most of the wasted energy is directly delivered to the wheels. Consequently, the proposed control method, which makes use of the deviation between the accelerations of the wheel and the chassis directly, adjusts the output driving torque to constrain the wheel slip by:

This formula indicates that the calculation of the desired drive torque for anti-slip control requires only the wheel and chassis accelerations. Th* represents the torque distribution command from the upper yaw-moment control, which the driver demands.
Data fusion for reference acceleration
According to classical rigid body dynamics, it is inaccurate for Equation (8) to take the chassis acceleration as the reference for four independent wheels. Thus, to ensure the accuracy of the proposed control method, the reference accelerations of each wheel center, which are rigid on the vehicle body, are utilized to replace the chassis acceleration.
The reference accelerations are derived from measurable quantities, including the chassis longitudinal acceleration, the chassis lateral acceleration, and the yaw rate. In this study, an inertia sensor is installed at the vehicle center of mass, simultaneously measuring these physical quantities.
Taking the front left wheel as an example, as shown in Figure 2, O is the vehicle’s center of mass (CM); ax, ay and γ the longitudinal acceleration, lateral acceleration, and yaw rate of the chassis, respectively.
Let i be FL, FR, RL or RR i.e. four wheels; aωi represents the wheel acceleration; δ the steer angle of front two wheels; lOi the horizontal distance from the vehicle centroid to the wheel center; θi the intersection angle between lOi and the vehicle body side; and axi and ayi the longitudinal and lateral reference acceleration at each wheel center, respectively. As shown in Figure 2, the proposed steering kinematics is assumed under a left turn.
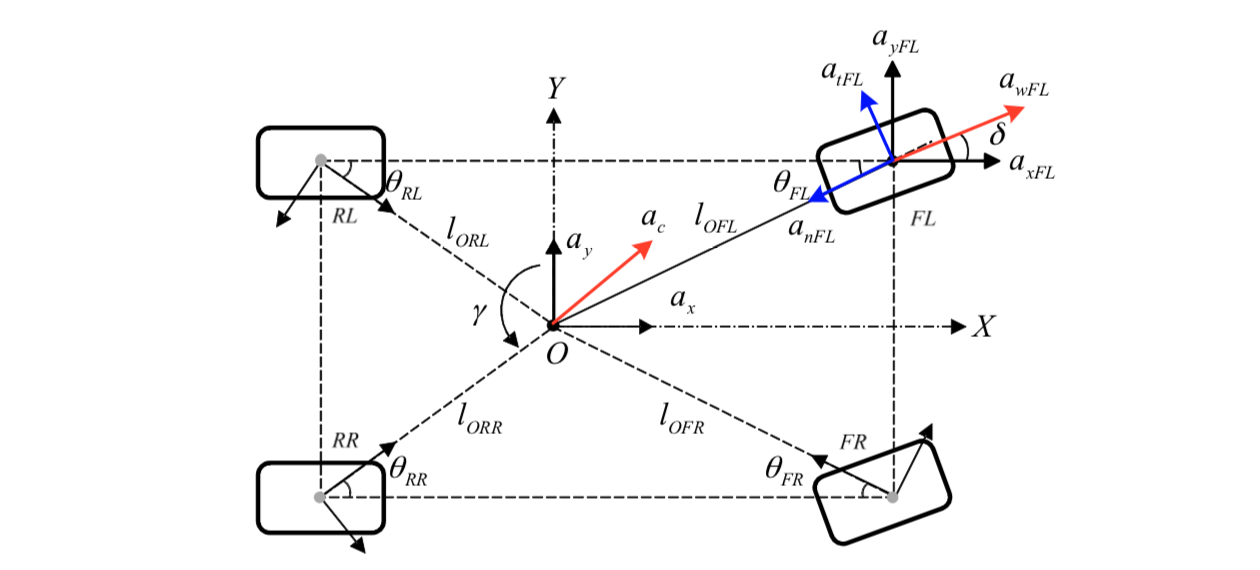
For each wheel, due to the rotation of the vehicle body, the reference wheel center acceleration comprises another two components besides the chassis ax and ay. As shown in Figure 2, they are the tangential and normal accelerations, i.e., ati and ani, defined as:

The reference acceleration axi and ayi of each wheel center can be calculated as:

Here, for a certain vehicle, the body parameters, e.g., lOi and θi, are fixed, with the inertia sensor installed at the vehicle center of mass. Additionally, the data fusion algorithm proposedignores the influences of the chassis vertical, pitching, and rolling motions. However, if higher calculation accuracy is required, all related quantities should be taken into account synthetically, which can be actualized by a sensor with 6DOF.
Proposed control scheme
The proposed wheel-slip control system is illustrated in Figure 3. As shown in Figure 2, the resultant reference acceleration has a different direction with the actual wheel acceleration, which indicates the wheel travel direction. Therefore the reference accelerations of each wheel center should be rewritten according to:
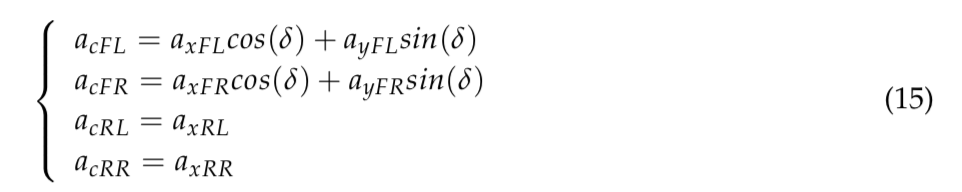
where δ represents the steer angle of both front wheels, which is measured by an angular sensor. The slight toe-out difference is neglected.
The actual wheel acceleration awi, achieved by taking the time derivative of the wheel speed Rωi, which is measured directly, should be equal or very close to aci, in the complete adhesion condition.
Then the eventual output torque is constrained by:
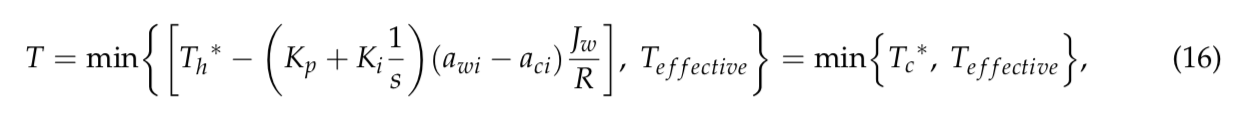
in which, Kp and Ki denote the PI compensator gains that ensure the wheel slip being controlled;
Teffective is the maximum non-slip output torque that the wheel can provide; T*h herein is a reference
command that represents the initial input torque requests from the driver. Herein, δ* is the actual
steering angle command given from the operator. From Equations (9) and (11), we can have T = Teffective + (T*h − T*c). Under the manipulation of the PI compensator, T*h − T*c ≈ 0. Consequently, the propulsion torque leads to T = Teffective.
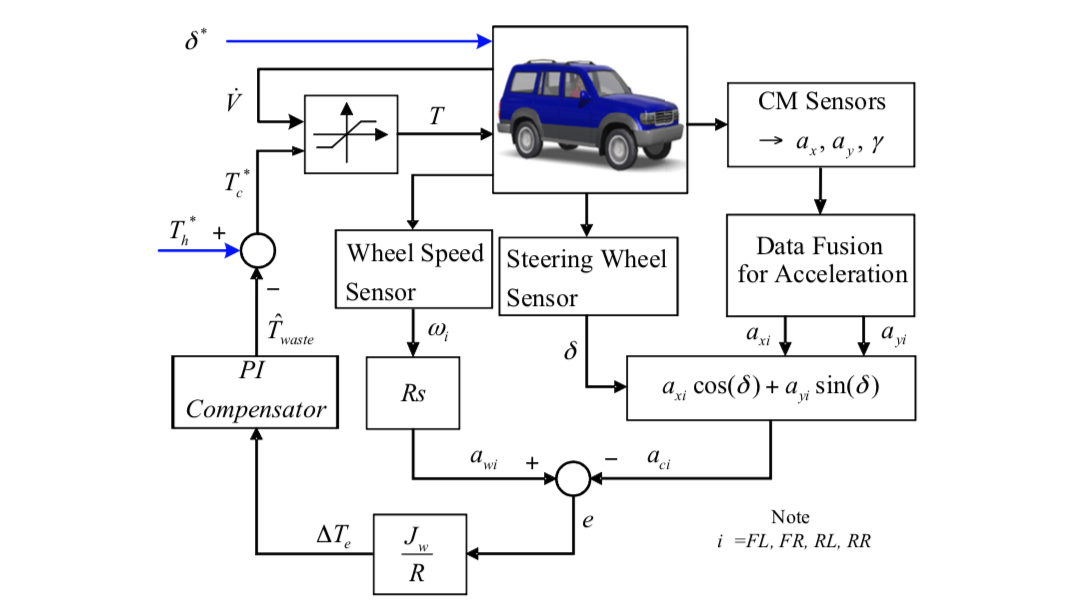
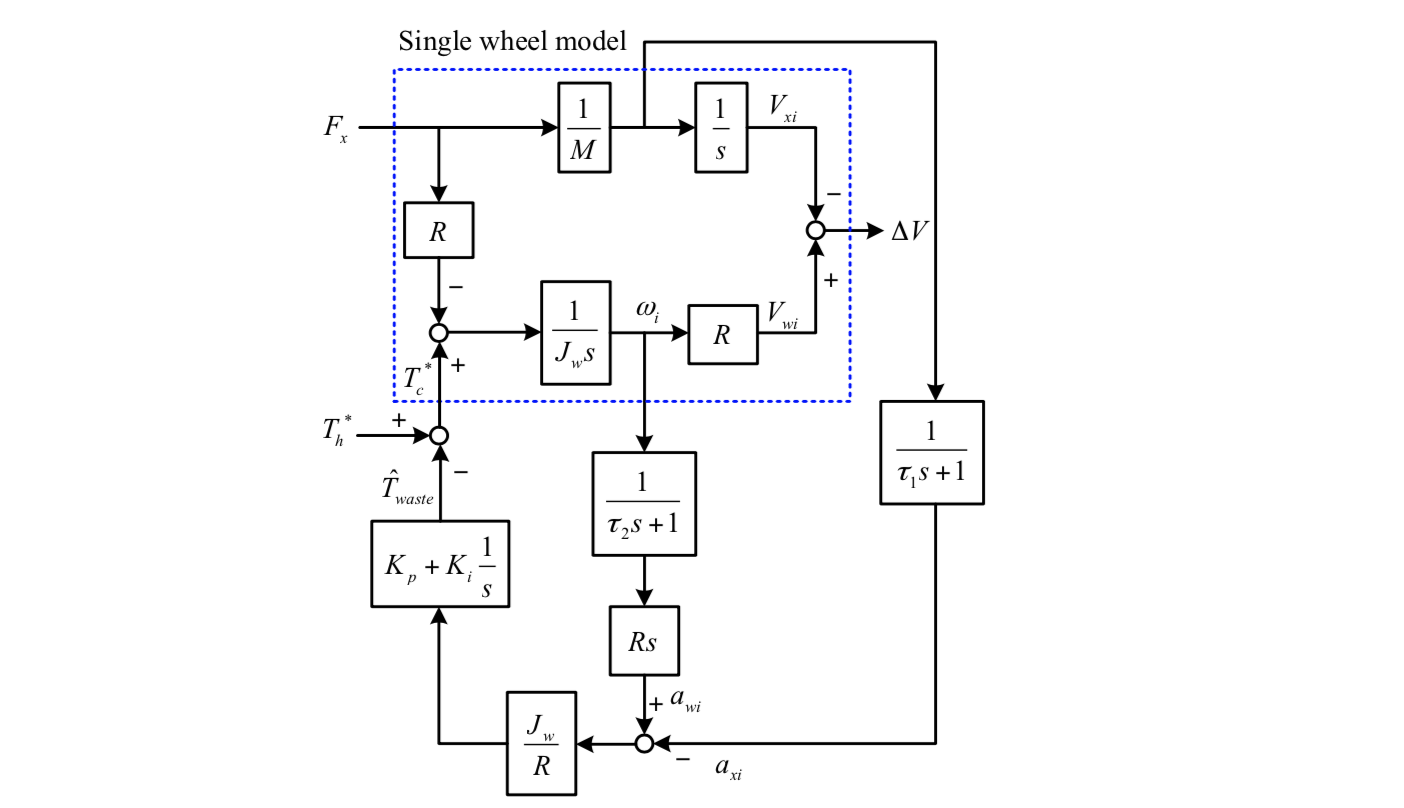
Basically, the proposed wheel-slip control is a kind of disturbance estimation. Its stability analysis is the same in each wheel. Based on the control block diagram of Figure 3 and the relevant motion equations, Figure 4 illustrates the equivalent model of the proposed control. Note that the driving resistance Fdr is assumed to be zero. τ1 and τ2 are the time constants for low-pass filters.
ΔV stands for the deterioration of wheel skidding. Vxi is the linear velocity of a quarter car. According to Mason’s gain formula, the following transfer functions can be obtained.
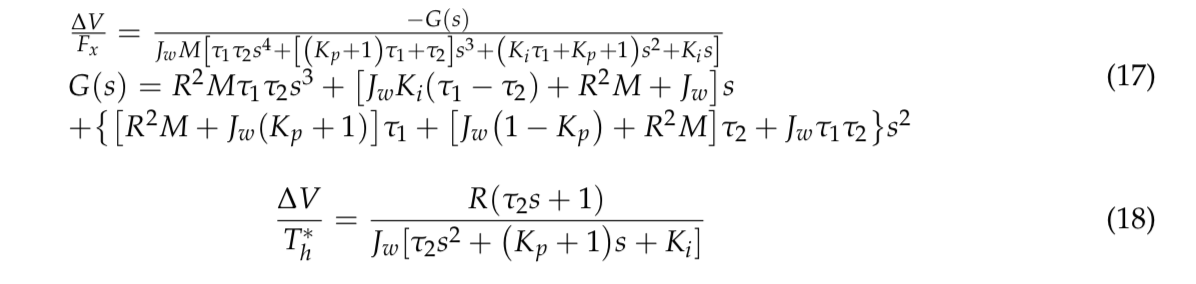
Equation (17) represents the transfer function of anti-slip control. According to the following Routh table
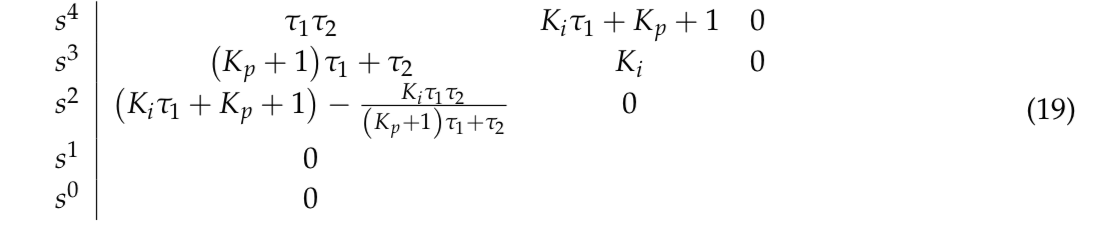
Hence, Equation (17) is stable if:
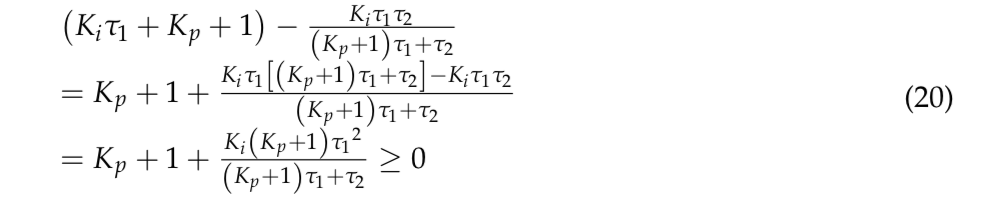
Clearly, the first column of the Routh table reveals that all numbers are positive. Hence, Equation (17) is stable. The second transfer function of Equation (18) shows the characteristic equation that:

Analyzing Equation (21) uncovers that the real part of the roots shall be negative numbers. Equation (18) is also stable in consequence. Since both Equations (17) and (18) are stable, it leads to the conclusion that the proposed wheel-slip control system is stable all the time.
Evaluation setups
To evaluate the performance of the proposed approach, this study applied software CarSim with Simulink to carry out the simulation. Table 2 shows the specifications of the test vehicle, which is a type of SUV. In addition, the powertrain of this vehicle was set in CarSim as “4-wheel Energies 2017, 10, 461 8 of 24 drive with all external powertrain components”. Hence, the electric motors are set in Simulink. In this configuration, the testing electric vehicle is fully power-decentralized, which can be used in the evaluation of the proposed sensor fusion strategy. Note that, in the simulations, the test vehicle is regarded as a rigid body and the maximum wheel steering angle is 36°. Three types of tests are carried out for the evaluations.

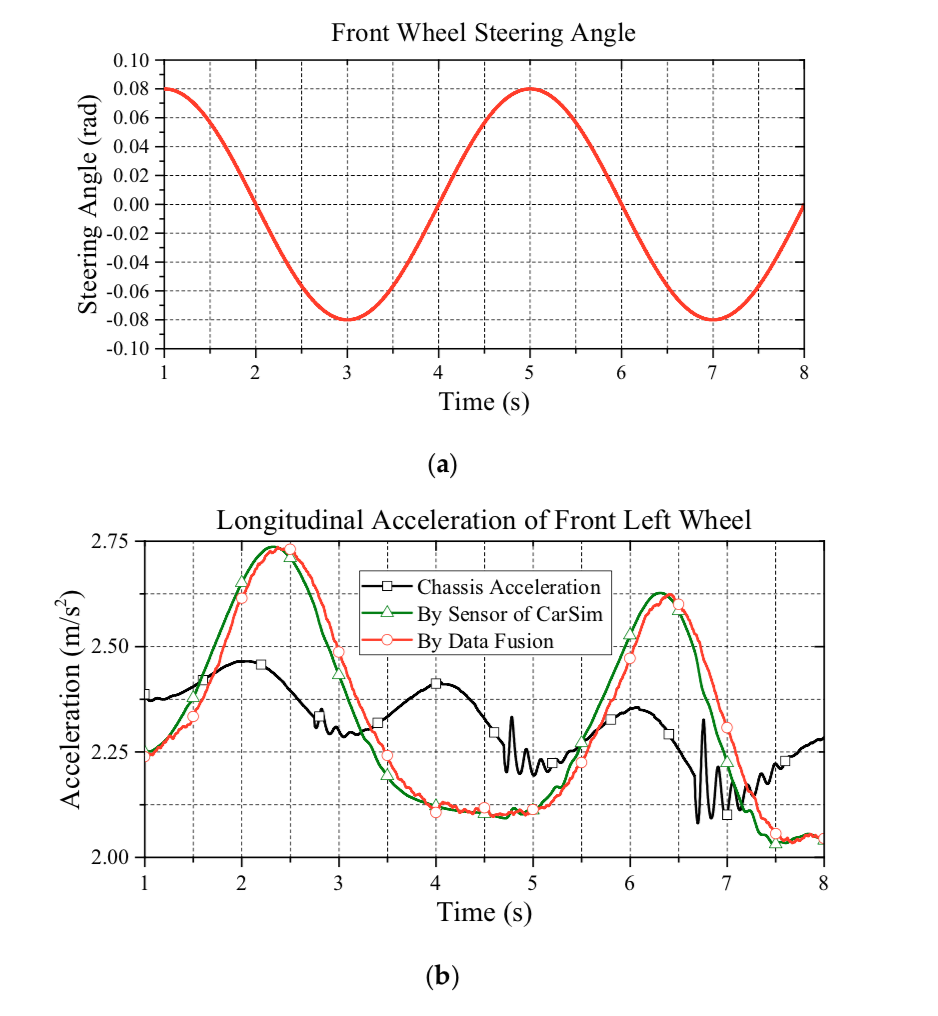
The first test is the verification of the proposed data fusion algorithm. The test conditions are an initial speed of 50km/h (31mph) and a road friction coefficient of 0.85. The front wheel steering angle is maneuvered as seen in Figure 5. To evaluate the effectiveness of the proposed data fusion algorithm, four acceleration sensors are installed at the center of four wheels in CarSim.

The second test is made under a defined double lane change (DLC). This test maneuver is performed to verify the effectiveness of the proposed wheel-slip control. The DLC test is recognized as a benchmark for evaluating steering stability, e.g. the international standard ISO 3888-2. To eliminate the randomness of the driver’s actions, a built-in UMTRI preview driver, which simulates an average driver in CarSim, is set to make the steering decision for trajectory tracking; the preview time is 0.5s. All tests are set to the same value for fair comparison. The initial speed for the DLC test is 38km/h (24mph), and two road friction coefficients are set to 0.8 and 0.45. The maximum output torque of each wheel is 500Nm. Note that the PI compensator gains in Figure 3 are set to Kp = 148 and Ki = 0.1. Regardless of the scenario, the PI gains are always set to the same value in the evaluations.
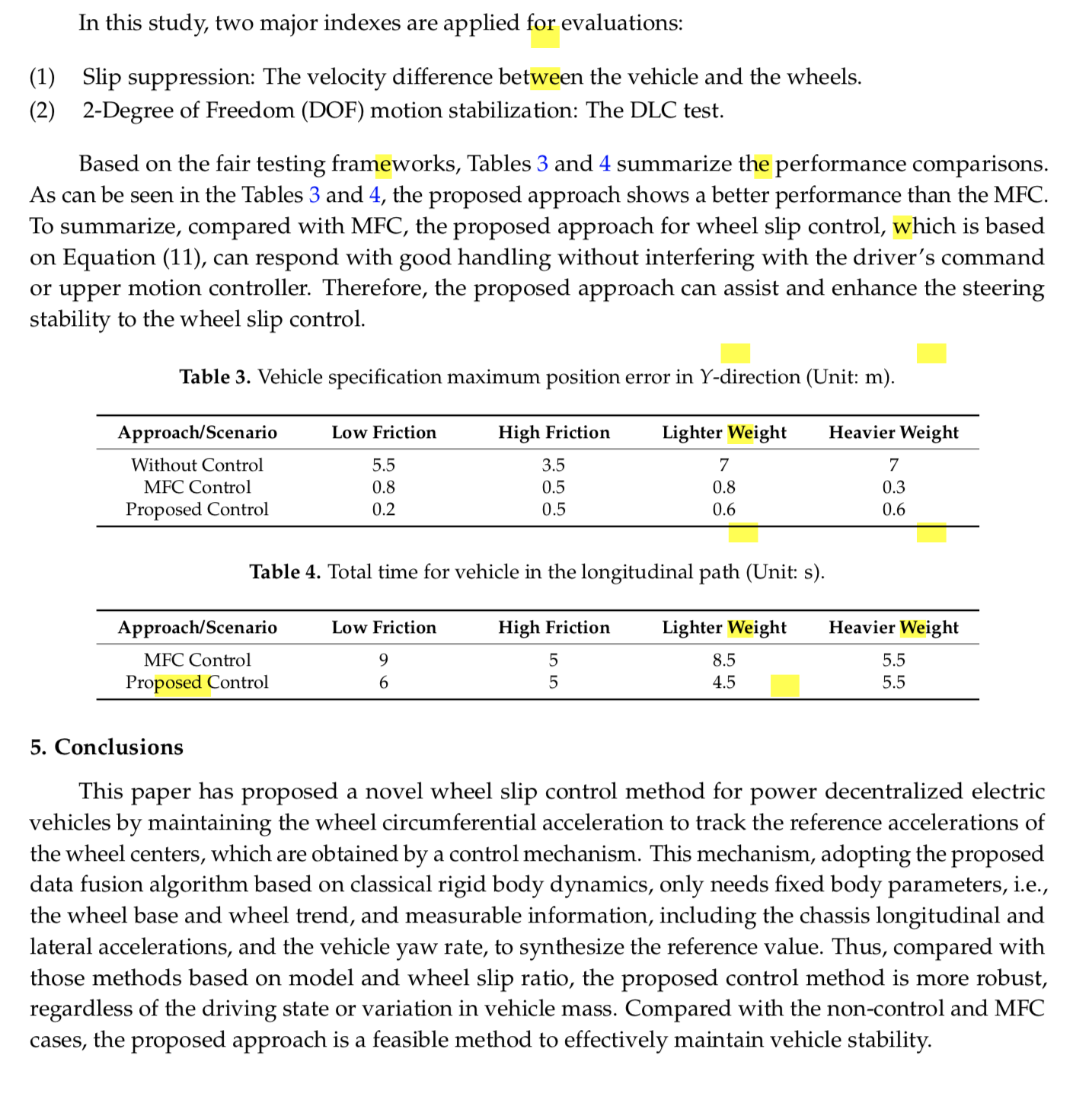
The third test verifies the robustness of lighter and heavier vehicle masses. This test is carried out on the DLC test with vehicle weights of 1,589kg and 1,939kg, respectively. The results of this test help evaluate the robustness of the proposed approach when the vehicle’s mass is changed.
Results and discussion
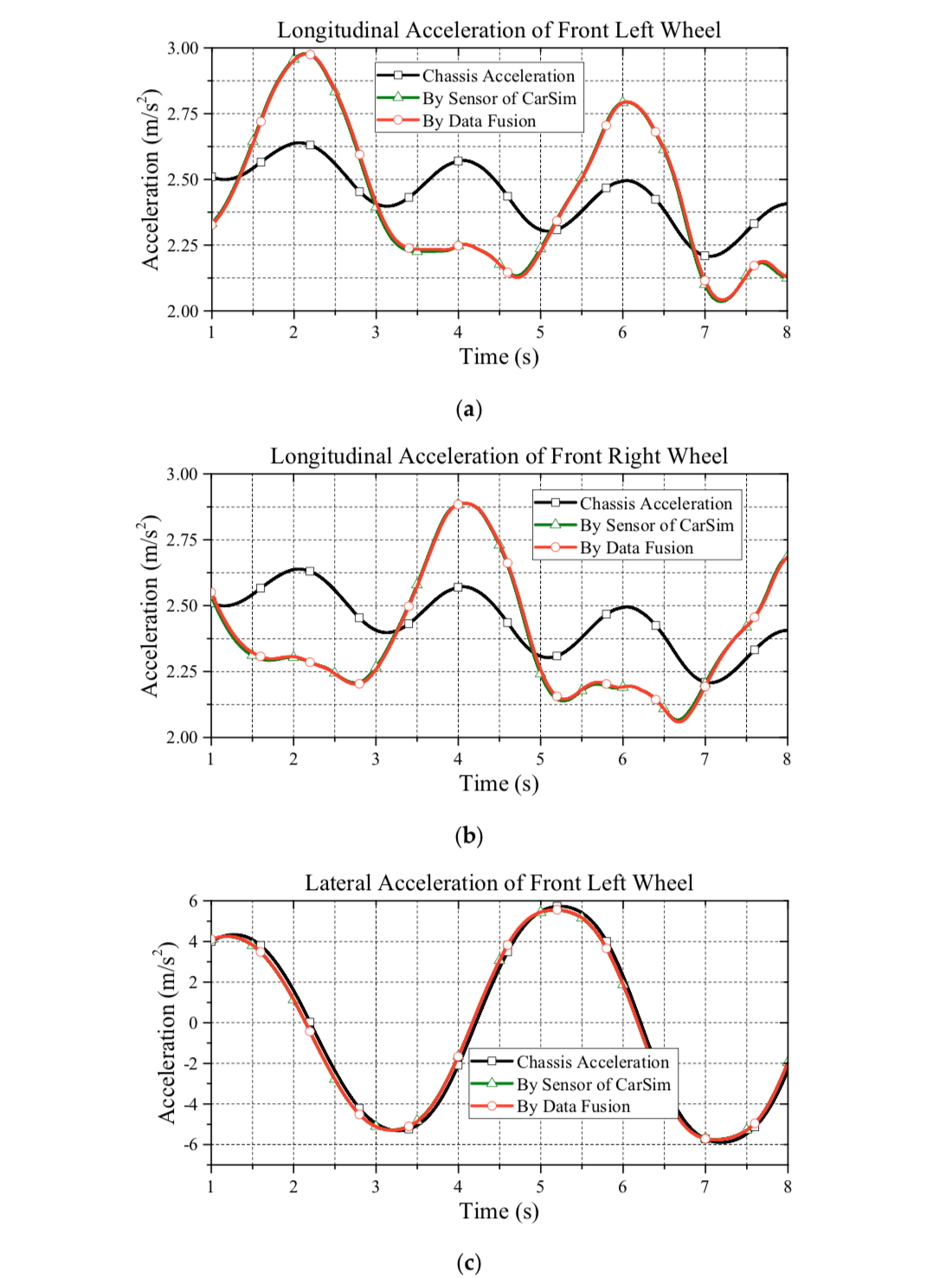
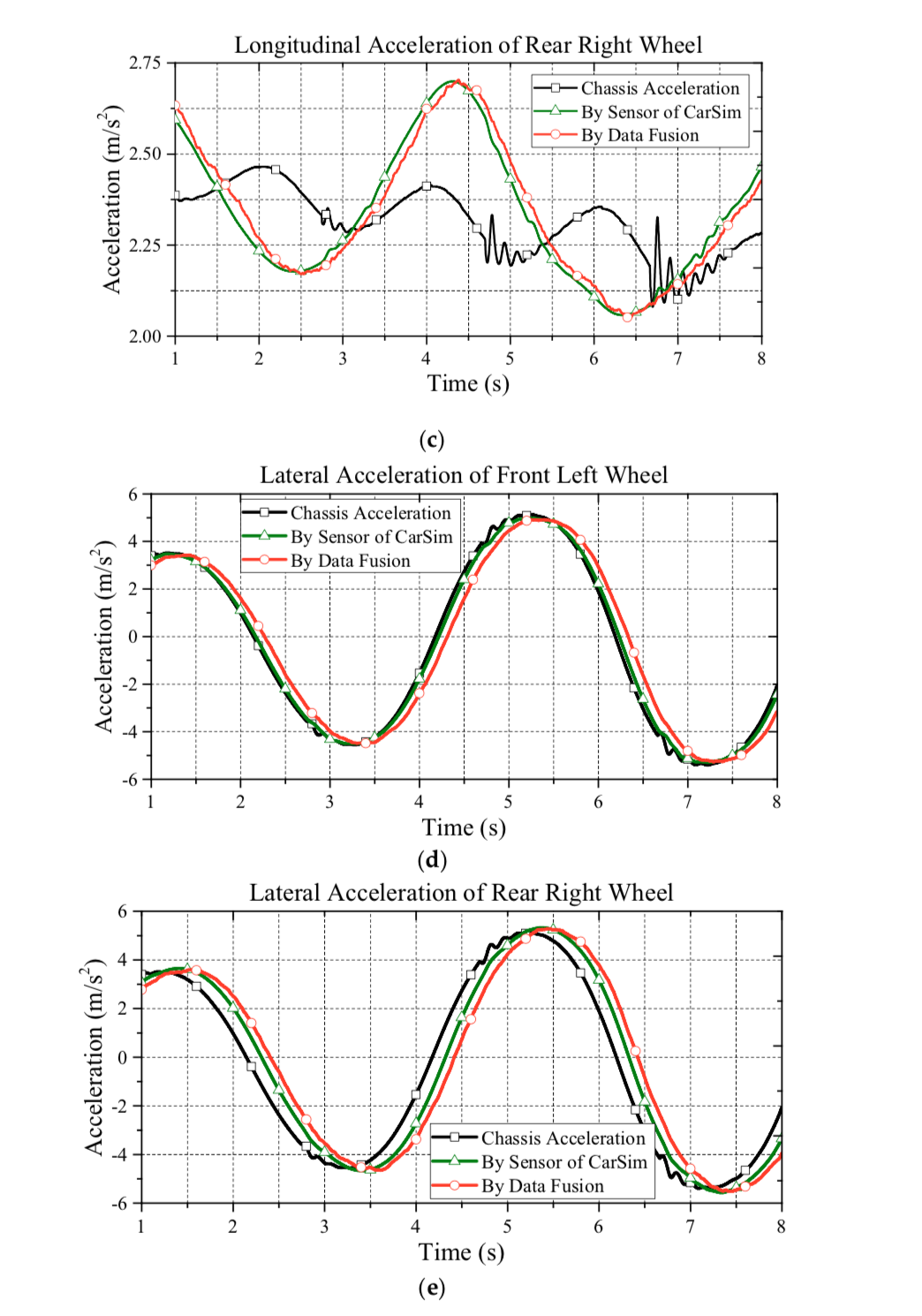
This paper presents a wheel slip control scheme based on the proposed data fusion algorithm. In the following, the aforementioned issues will be verified under the corresponding simulations. In order to verify the wheel slip control, the data fusion performance is firstly evaluated. Note that based on the steering command of Figure 5, Figure 6 shows the simulation results of data fusion as based on the steering command of Figure 5, Figure 6 shows the simulation results of data fusion as they pertain to the front wheels. Compared to the proposed estimation with the information from sensors, as can be seen in this figure, the proposed approach for acceleration estimation is reliable.
Additionally, considering the cost of the chassis acceleration sensor, the proposed approach is a cost-effective solution. Moreover, in this simulation, we can also observe the acceleration discrepancy between the CM and individual wheels. Therefore, without the data fusion from all wheels, using the acceleration information from a single wheel instead of chassis acceleration is not recommended.
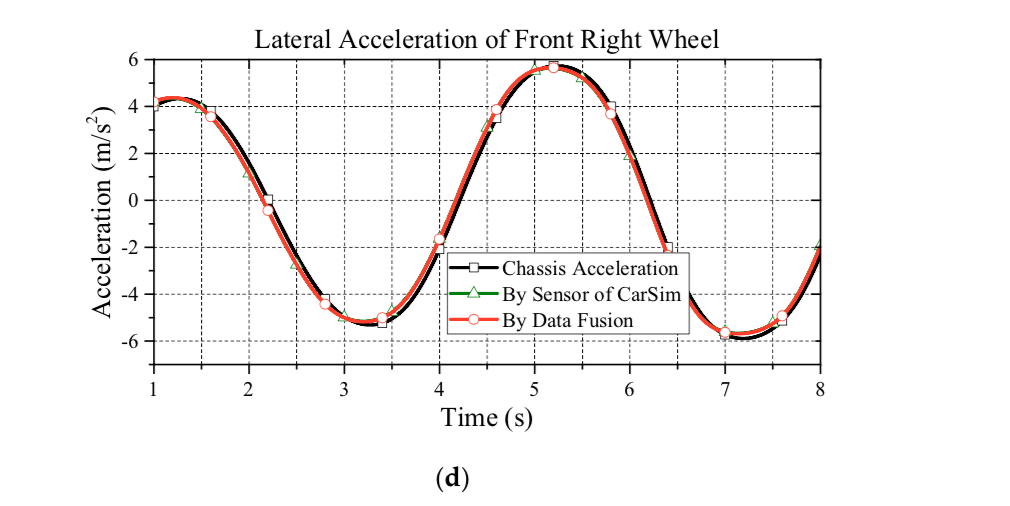
In order to evaluate performance of the proposed data fusion under a noisy environment, a mechanism of white noise is added in the feedback states. The noise is added on measured data of each wheel according to the data from a real sensor: Tamagawa AU7428N200 (Tamagawa Seiki Co Ltd, Nagano Prefecture, Japan). The noise for acceleration on the CM is up to 0.049m/s . The noise for the yaw rate is up to 1 deg/s. The noise effect for the wheel speed occurs up to 15 rpm. Figure 7 shows the comparative results. As can be seen in this figure, the proposed data fusion algorithm shows acceptable performance against the effect of noise.
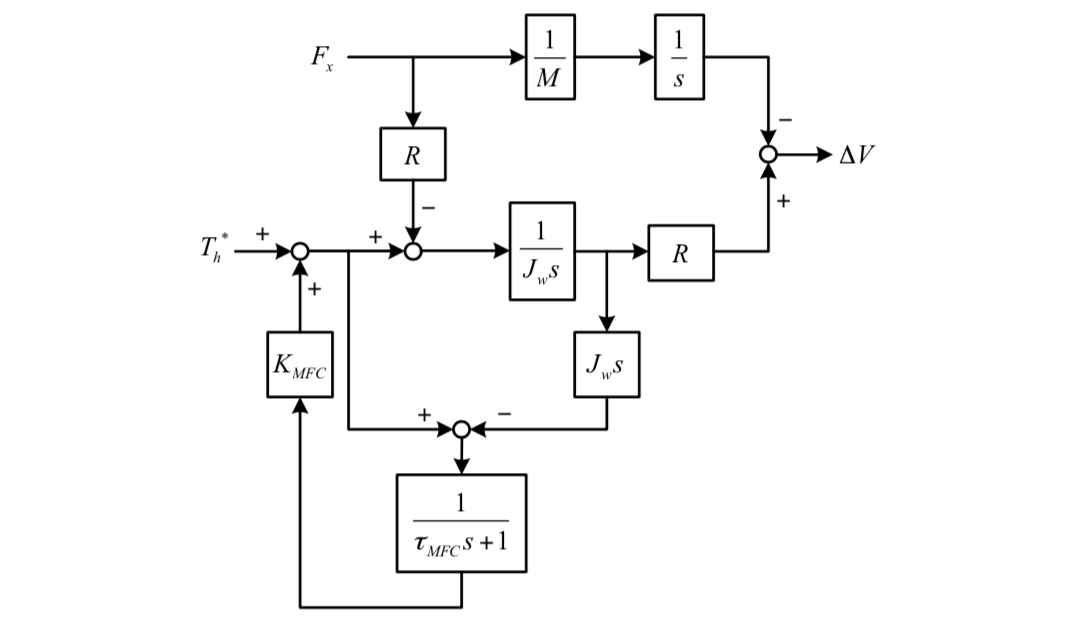
According to [8], a rival MFC approach is employed for performance comparison, for which the control block diagram is depicted in Figure 8. In this figure, the KMFC should satisfy the following control block diagram is depicted in Figure 8. In this figure, the KMFC should satisfy the following stability condition:

Note that the minimum of KMFC is KMFC–min =0.0144. In this paper, we set KMFC = 18. TMFC is the time constant of the low-pass filter.
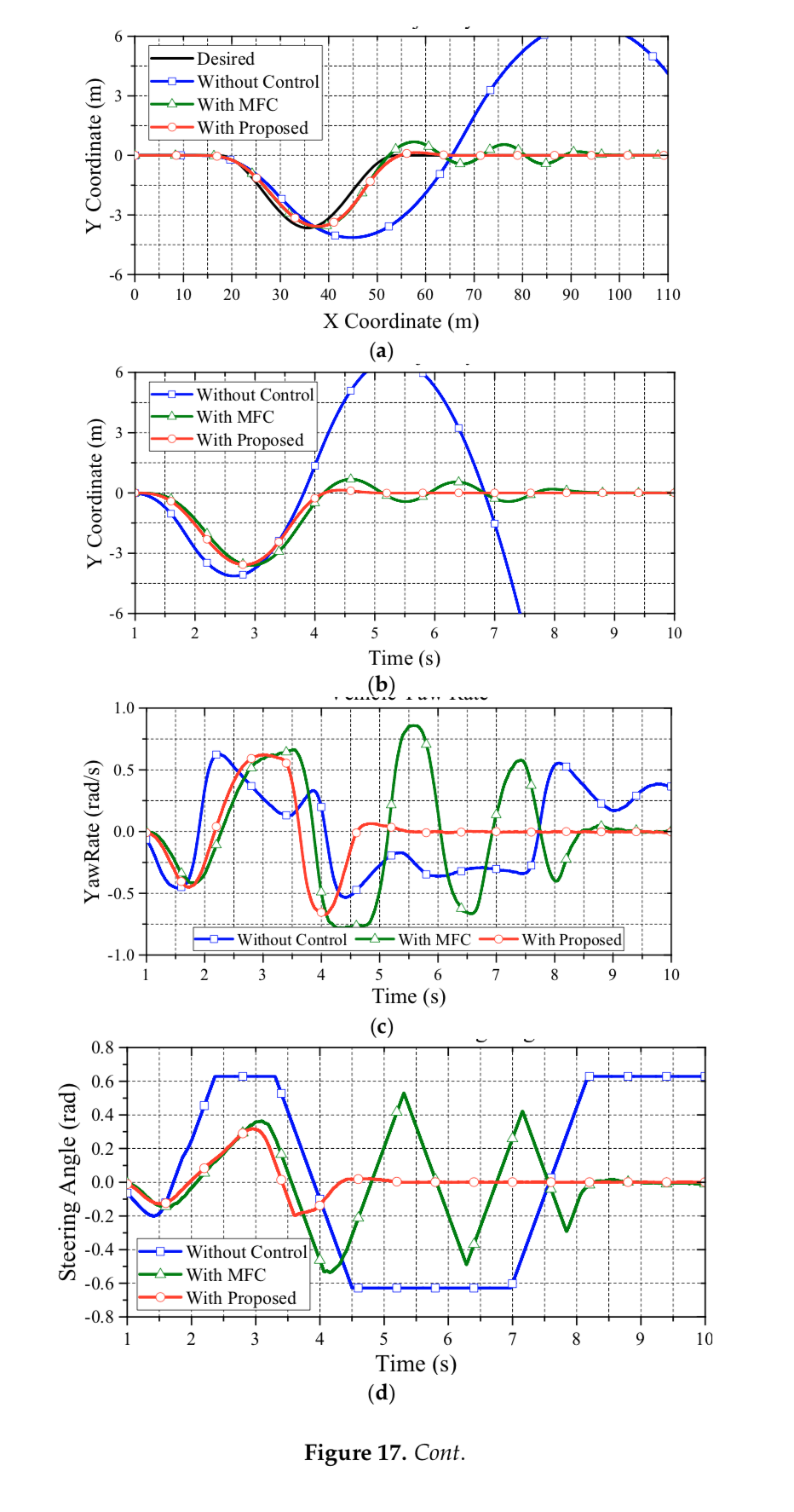
Based on the reliable foundation of proposed data fusion of the acceleration estimation, the performance of the wheel slip control can be evaluated. In order to fairly observe the performance differences from all approaches, the upper control of ESC is turned off in CarSim. In the following, the second test with high and low friction coefficients are evaluated. Figure 9 reveals the main comparisons of the trajectory from the DLC test under the friction coefficient of 0.8. Clearly, the vehicle without control and the vehicle with MFC cannot pass the DLC test, while the vehicle with the proposed control can follow the desired trajectory smoothly.
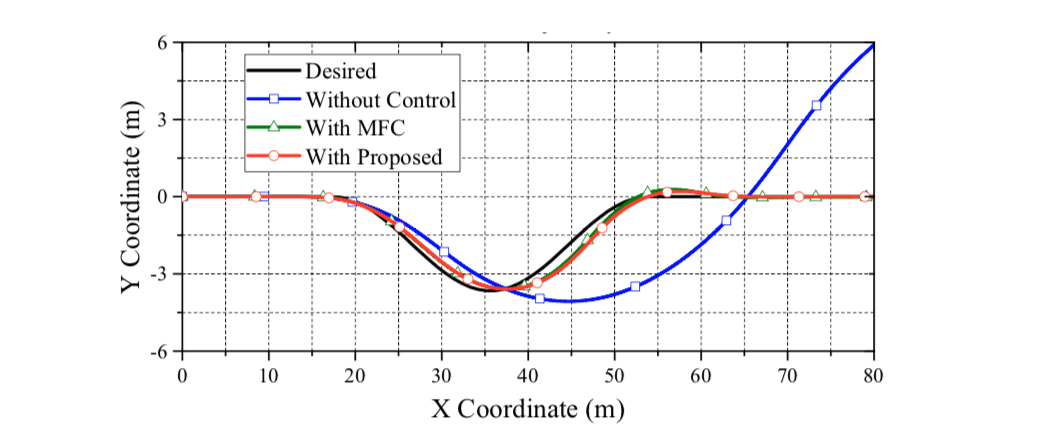
Figure 10 shows the yaw rate of the vehicle in the DLC test. As can be seen in this figure, vehicle without control presents a largish oscillatory response, which means a poor handling performance. Only the proposed data fusion approach with PI compensation can achieve a good dynamic response on yaw rate. Based on Figure 9, the proposed approach can lead the vehicle back to a straight driving path with zero yaw rate in a short time. This is because the achieved wheel slip control ensures longitudinal and lateral tire force, which enhances the yaw stability on slippery road surfaces. Figure 11 reveals the front wheel steering angle of the DLC test. Note that the reduction ratio of the steering angle between the operator and front wheels is 20:1. As can be seen in this test, only the proposed approach can nimbly steer the vehicle through the DLC with nimble turning. The MFC and non-control cases both reach the maximum wheel steering angle (i.e., 36°) and cause a saturating deterioration.
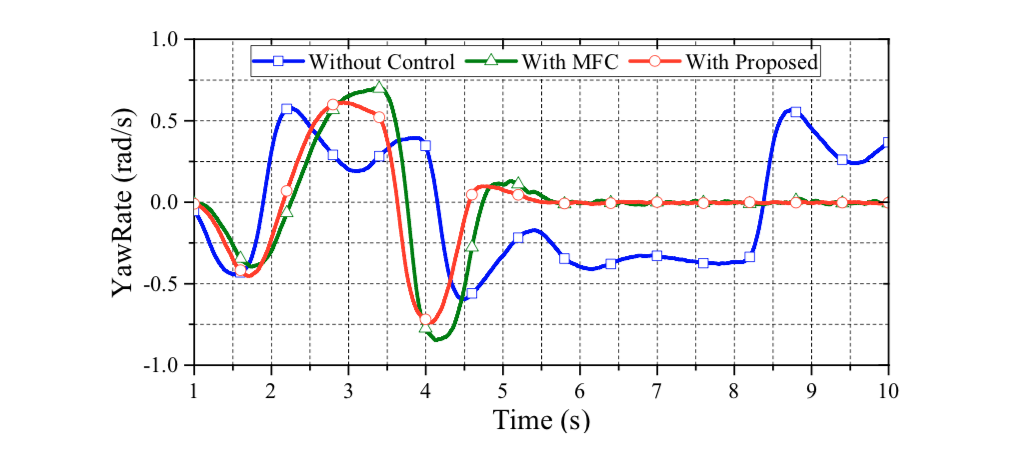
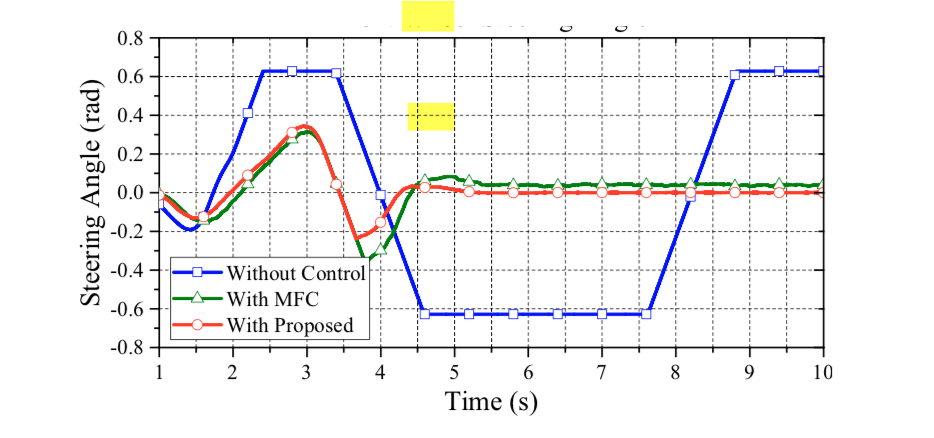
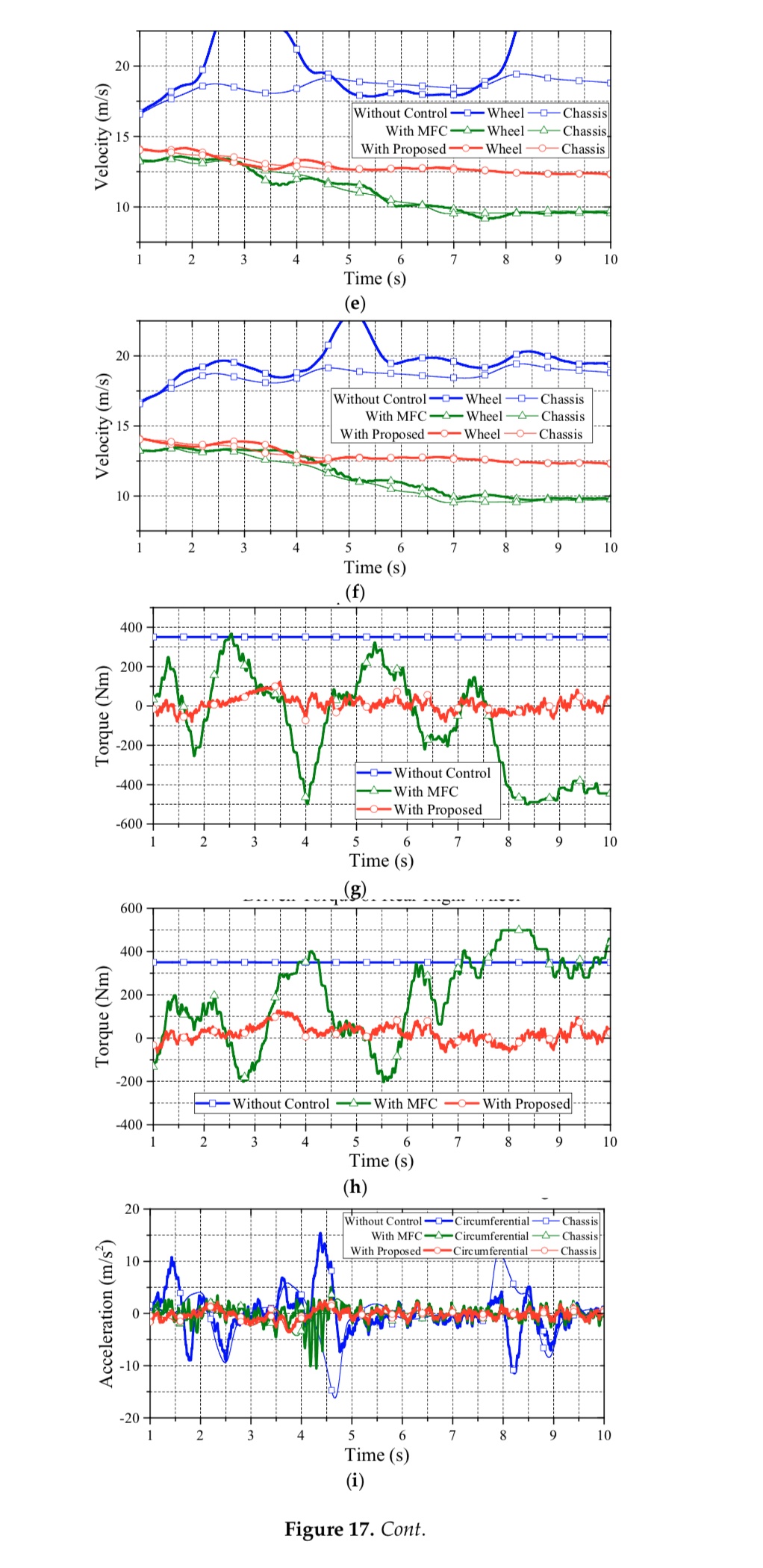
Figure 12 illustrates the comparisons of wheel velocity and chassis velocity. As seen in this figure, the proposed approach has a reliable performance on wheel slip suspression. Basically, withoutcontrol, the actual wheel acceleration cannot track the reference acceleration of each wheel center, and the vehicle accelerates and decelerates drastically on the curve track. Consequently, the vehicle without control shows an apparent wheel slip. However, by reducing the difference between the actual and the reference accelerations, the vehicle with the proposed control can restrain the wheel slip effectively. Note that, in Figure 12, the MFC approach clearly prevents wheel slip by decreasing vehicle speed. Hence, although the MFC approach can suppress wheel slip, the tradeoff is the loss of kinetic energy; thus, the MFC approach, then, does not have a good dynamic performance due to the lack of driving torque.
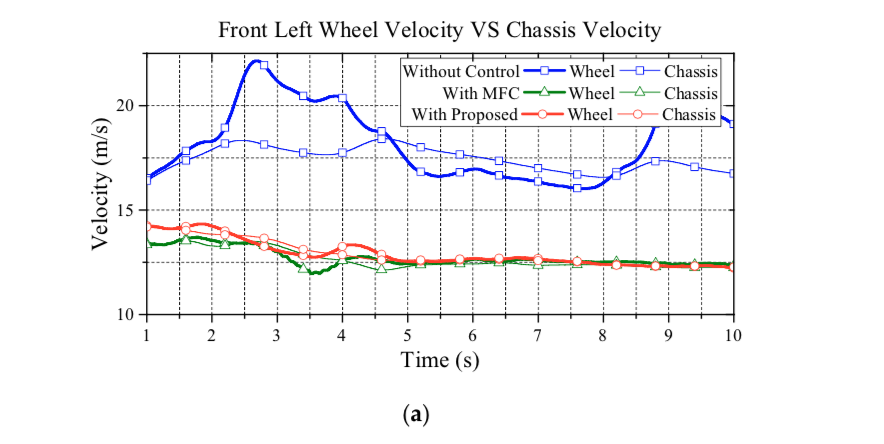
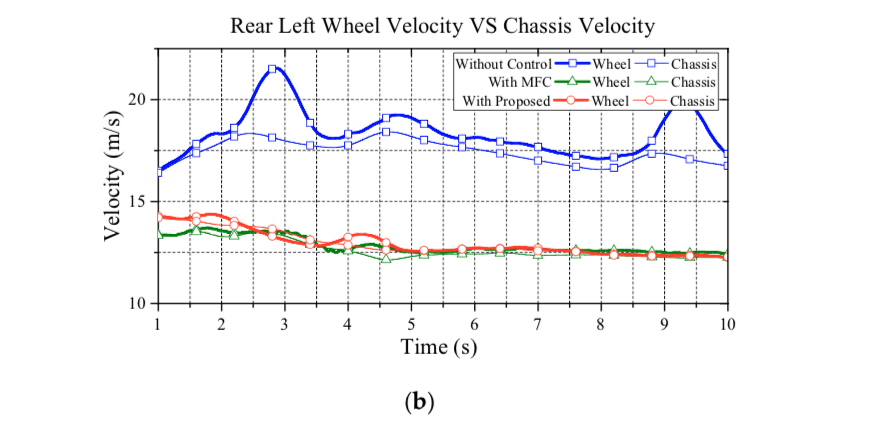
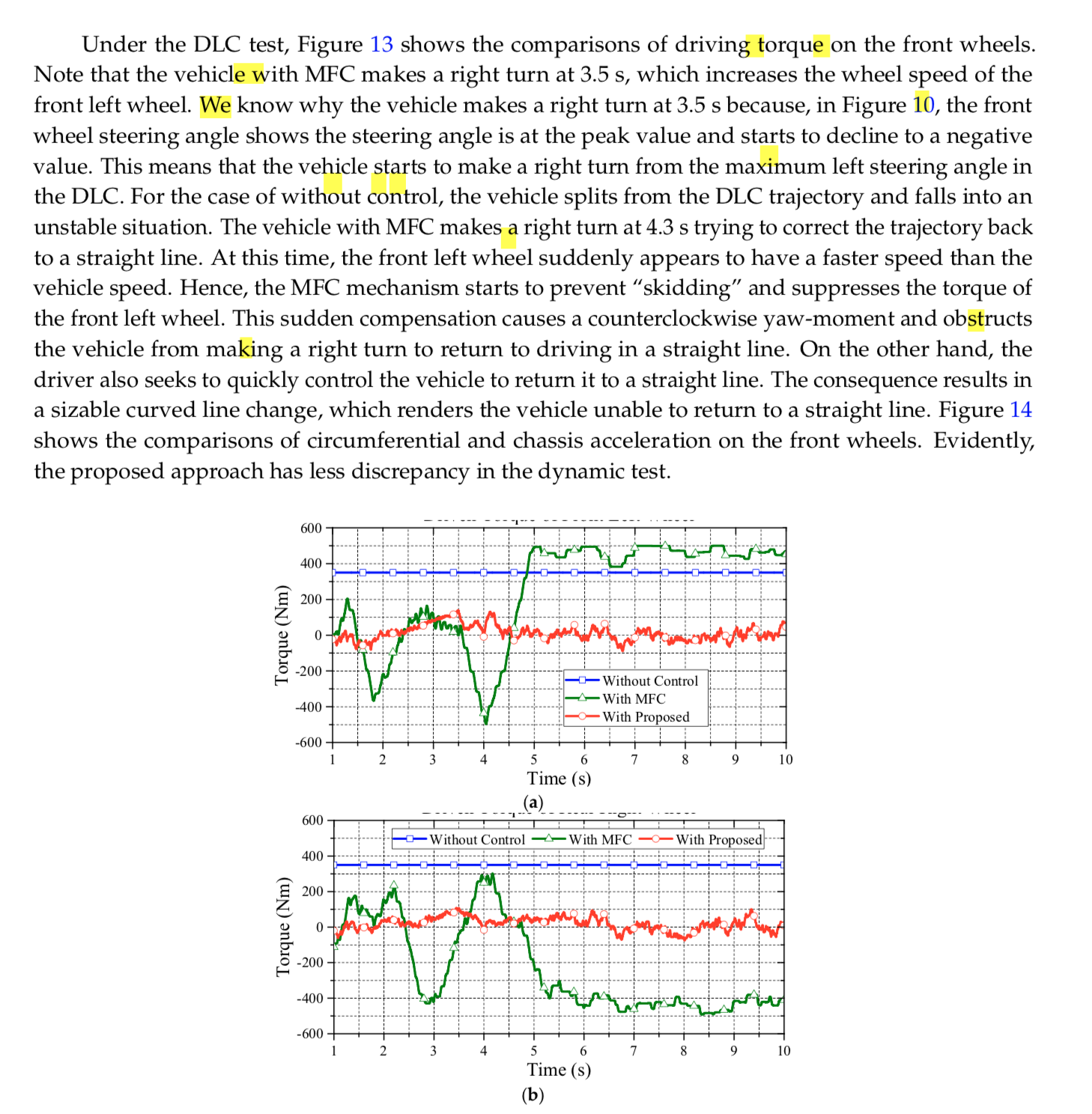
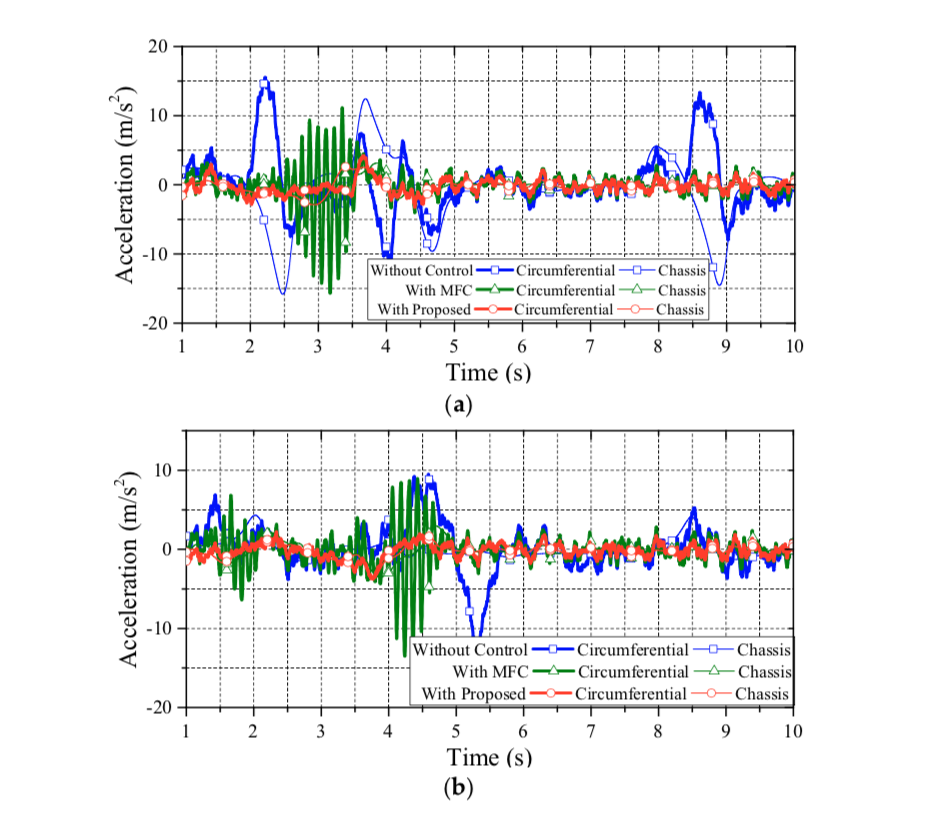
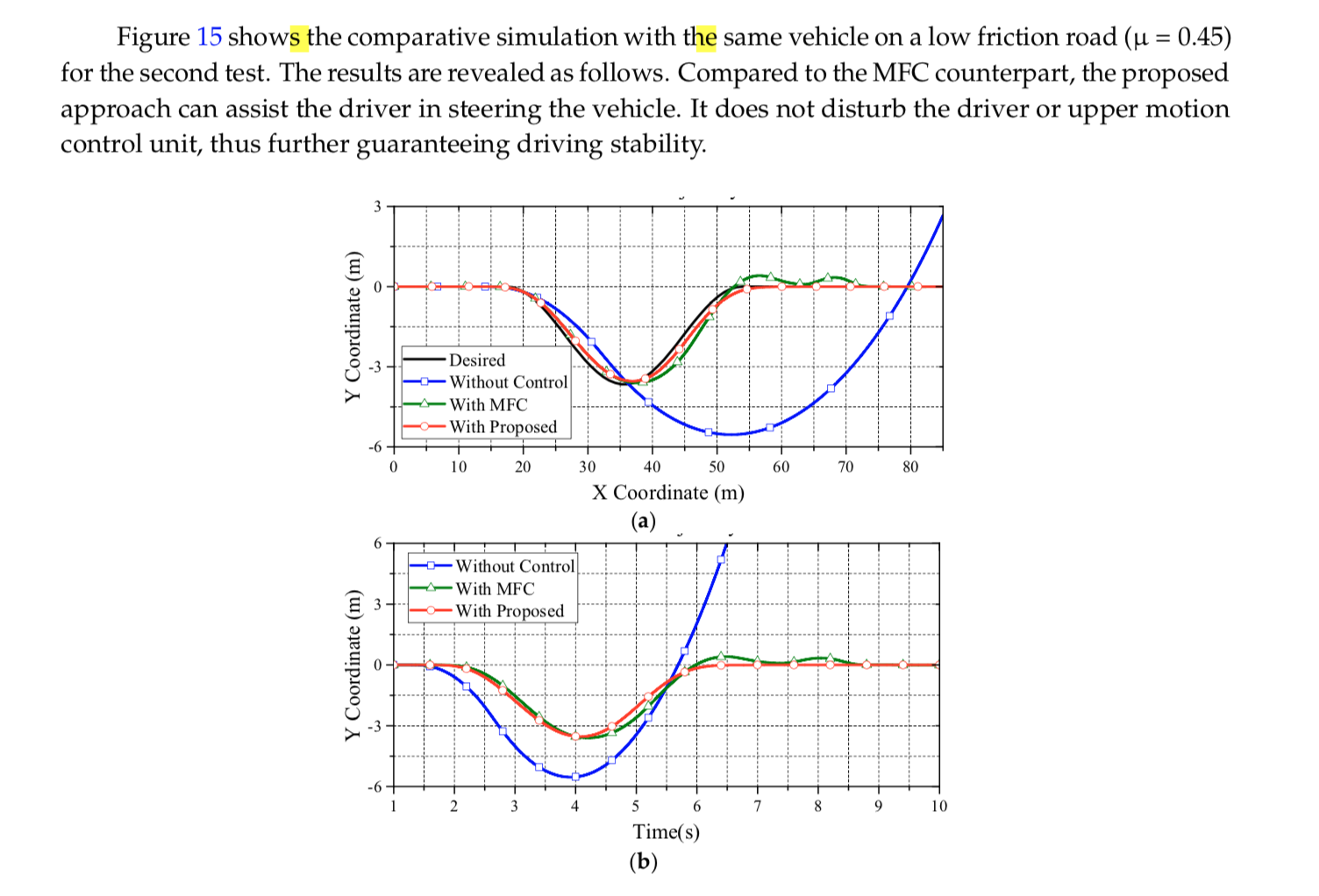
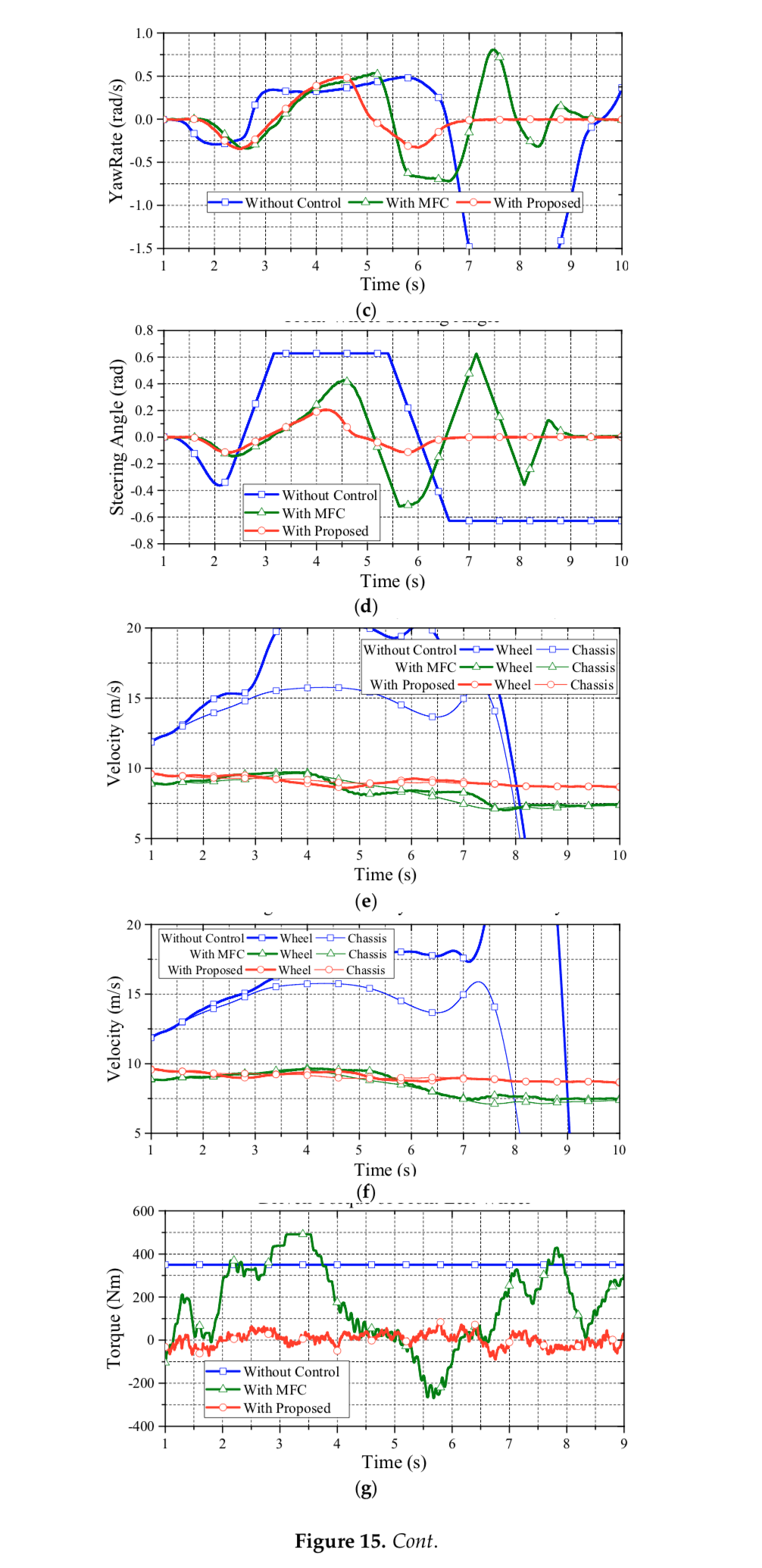
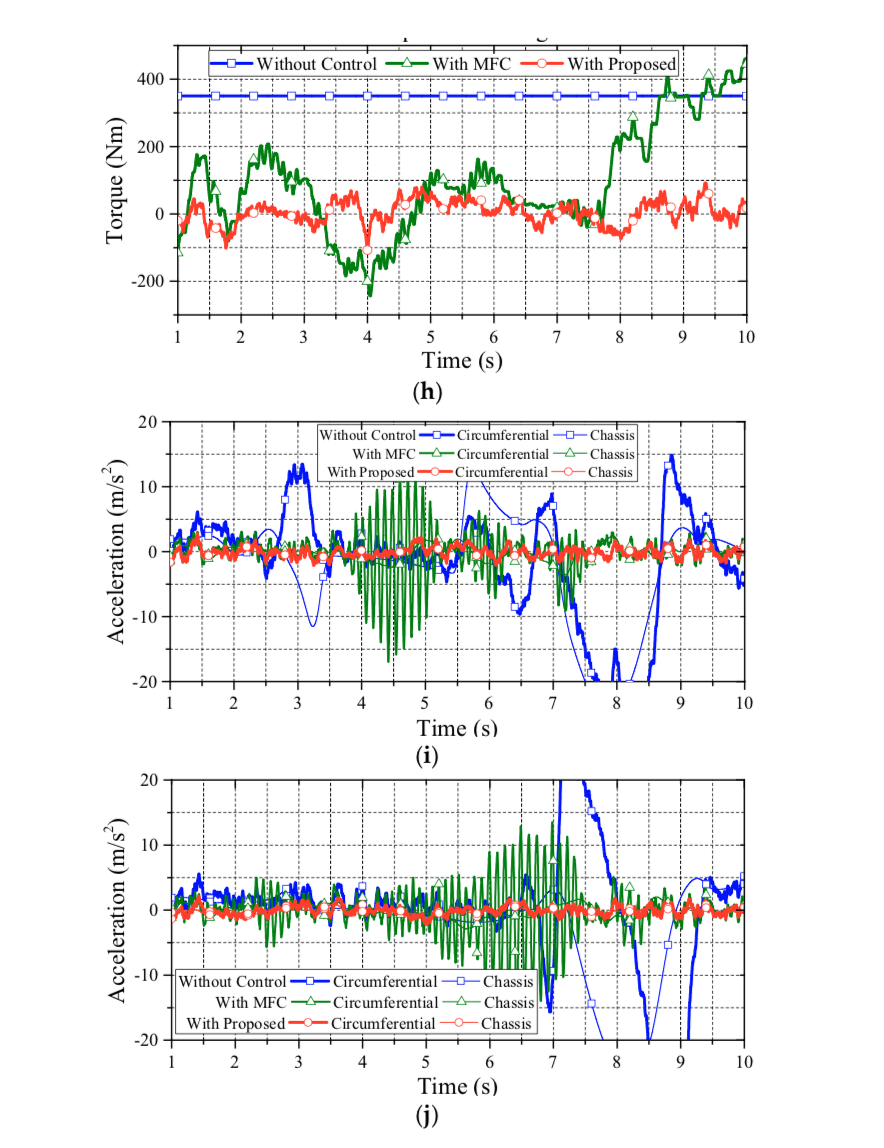
Figure 6 illustrates the third simulation for robustness evaluation. This evaluation is performed under the DLC test with a heavier vehicle mass of 1939 kg on a road friction coefficient of 0.8. The initial vehicle speed of this test is set to 54 km/h. The simulation results, which highlight that the proposed approach has achieved the claimed anti-slip performance not only on regular vehicle mass but also but also heavier ones, are as follows.
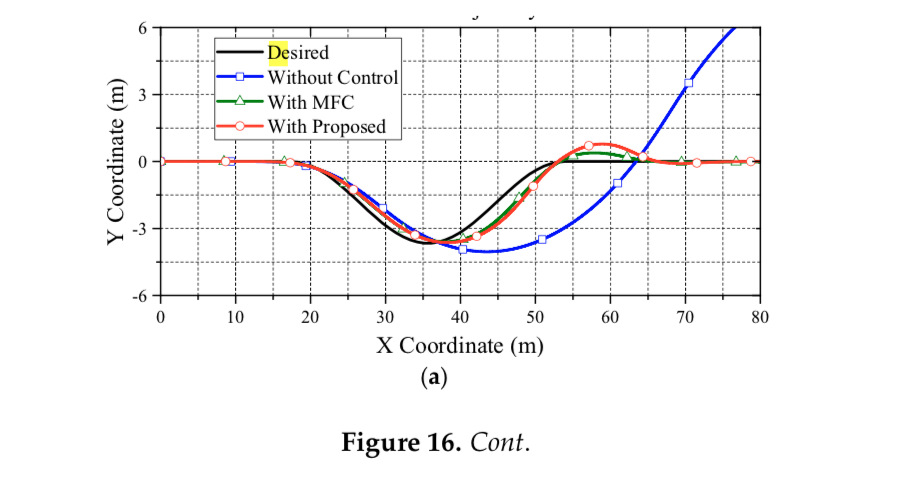
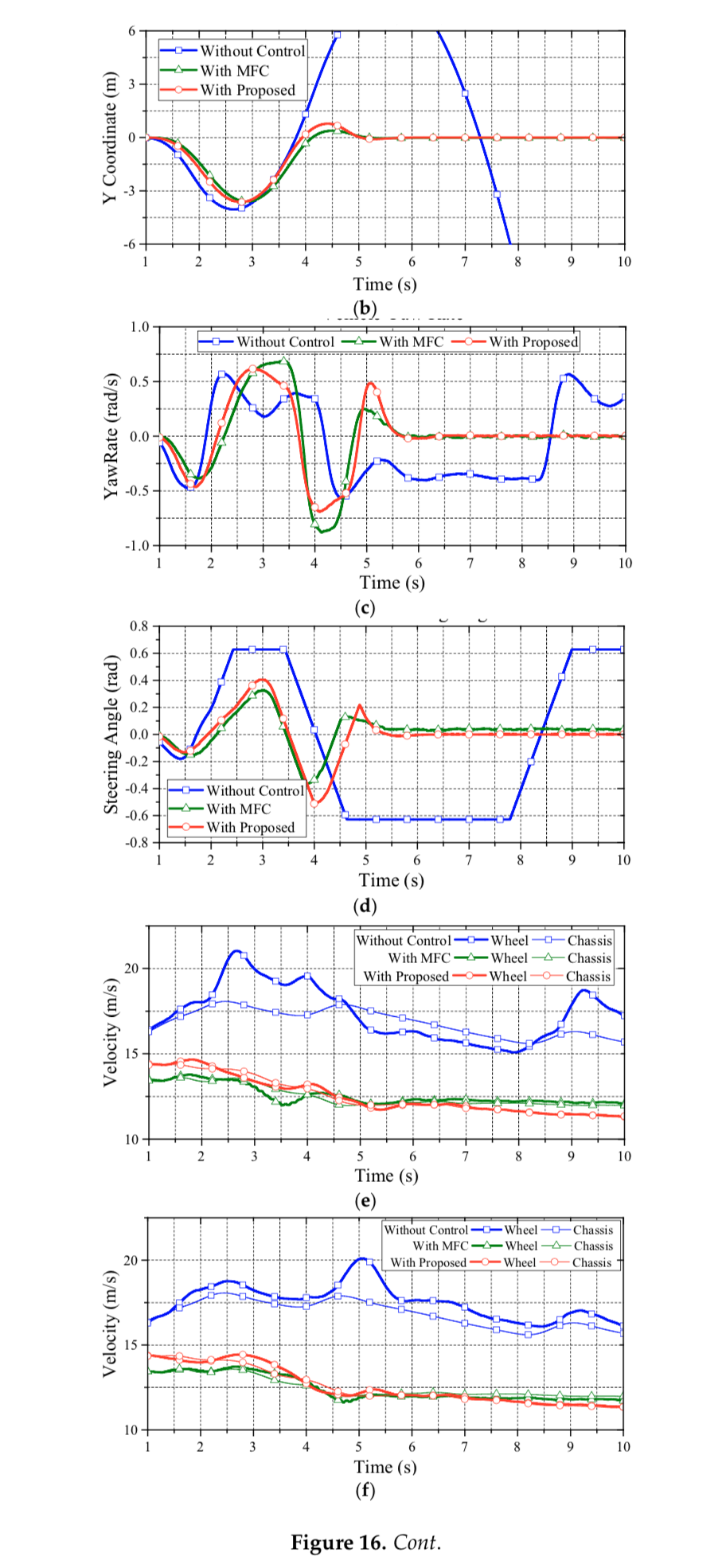
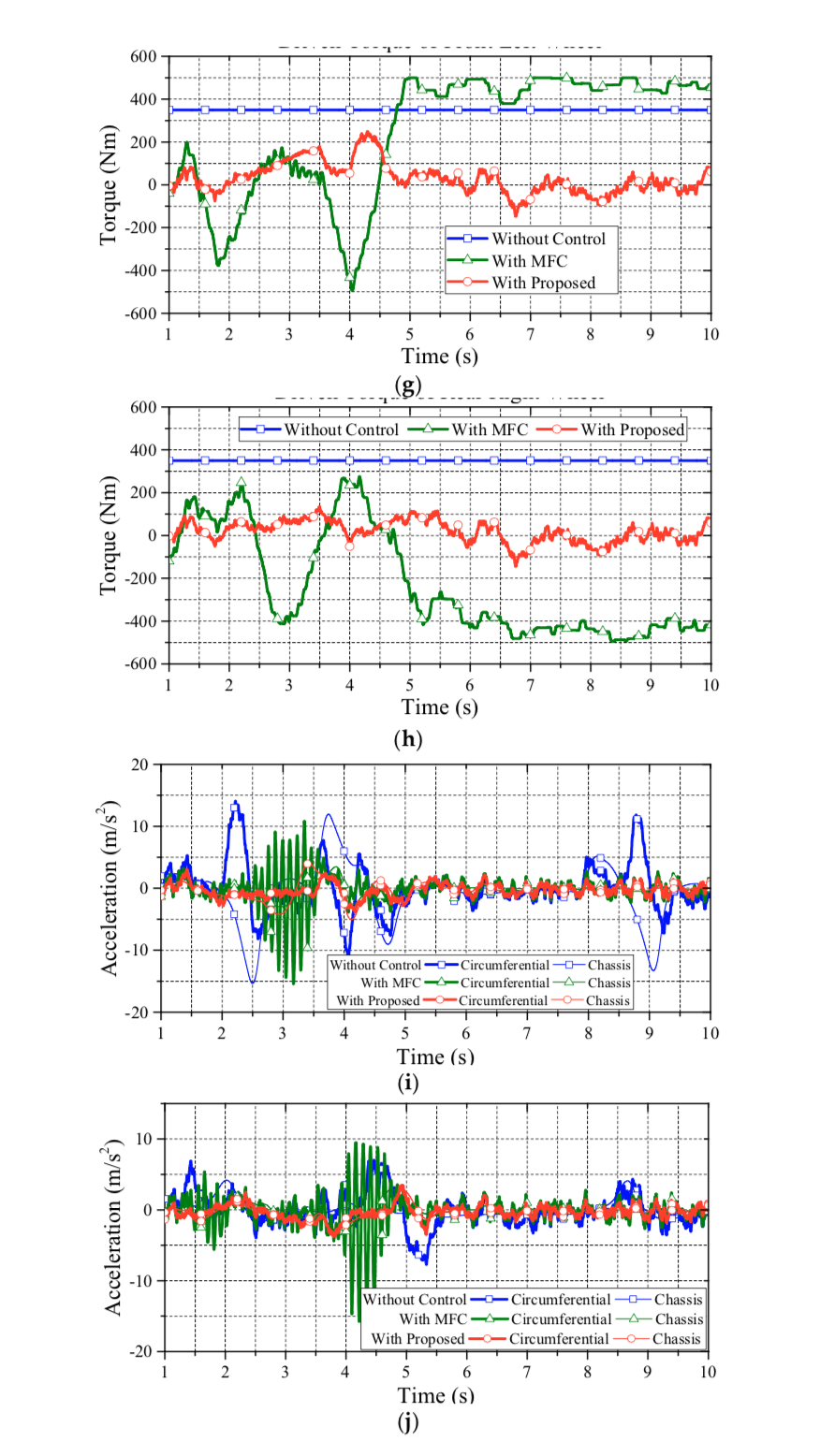
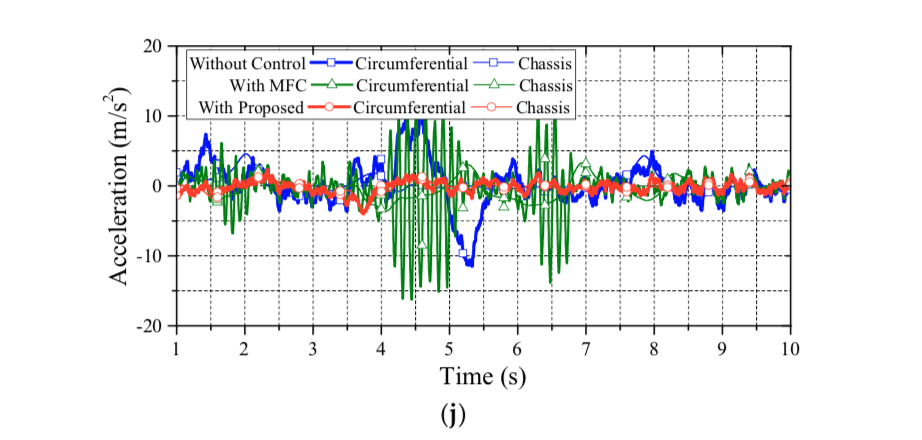
Figure 17 illustrates the evaluation of the DLC test on a lighter vehicle mass of 1,589kg. The testing road friction coefficient is set to 0.8. The initial vehicle speed of this test is set to 54km/h. The simulation results also reveal that the proposed approach has the claimed anti-slip performance on lighter vehicles. Note that, in Figures 15–17, three vehicle masses are evaluated: 1,589kg, 1,789kg and 1,939kg, respectively. These scenarios stand for the case of one driver, one driver with two passengers, and one driver with four passengers. The simulation results reveal that the mass perturbation has deep influences on MFC.